Założenie o rozkładzie normalnym zmiennych jest podstawą wielu klasycznych technik modelowania (przykładowo analiza wariancji, regresja gaussowska, modele mieszane). Stąd też popularność technik testowania tego założenia.
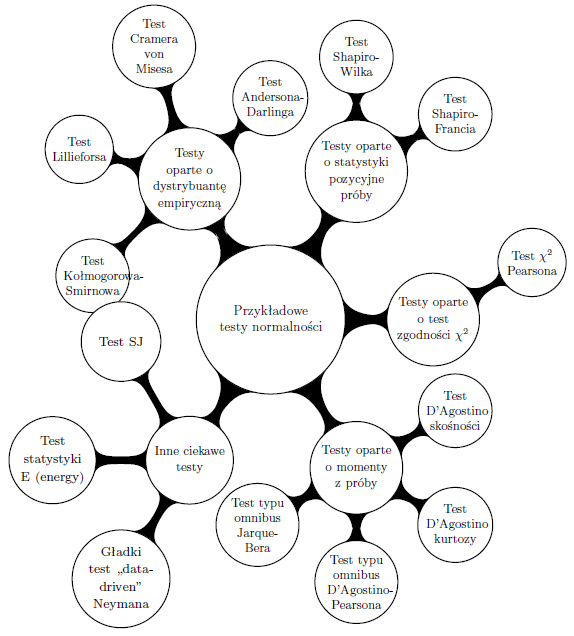
W tym dokumencie przedstawiamy czternaście przykładowych testów normalności podzielonych na pięć grup, różniących się sposobem konstrukcji statystyki testowej. Poniżej przedstawiono testy, które mnie osobiście z różnych powodów interesowały, ale to nie są wszystkie testy do badania normalności. Moim celem było pokazanie mnogości podejść do tematu badania zgodności z rodziną rozkładów normalnych a nie wykonanie pełnego przeglądu testów normalności.
Ten dokument był częścią materiałów przygotowanych w ramach szkolenia o testach dla KNFu, a po uzupełnieniu i za zgodą został przekazany fundacji SmarterPoland.pl. Za pomoc w uzupełnieniu i rozbudowaniu pierwszej wersji dziękuję Krzysztofowi Trajkowskiemu, który jak zwykle wskazał wiele punktów, które warto poprawić i testów o których warto napisać.
Mam nadzieję, że dokument okaże się przydatnym. Wszelkie komentarze, sugestie propozycje do tego dokumentu proszę zgłaszać na adres Przemyslaw.Biecek@gmail.com. Z dokumentu można korzystać na zasadzie uznania autorstwa, cytując:
Przemysław Biecek, Wybrane testy normalności, 2013. Materiały Fundacji SmarterPoland.pl.

Interesuje nas testowanie zgodności z rodziną rozkładów normalnych. Obserwujemy próbę prostą ![]() obserwacji
obserwacji ![]() ,
, ![]() , niezależnych realizacji zmiennej losowej o rozkładzie
, niezależnych realizacji zmiennej losowej o rozkładzie ![]() . Interesuje nas weryfikacja hipotezy
. Interesuje nas weryfikacja hipotezy
Ponieważ parametrów ![]() i
i ![]() najczęściej nie znamy, więc testowana hipoteza zerowa jest hipotezą złożoną, co nastręcza pewnych trudności. W poniżej opisanych testach najczęściej te parametry są estymowane z próby, z użyciem być może niestandardowych estymatorów, a statystyka testowa odpowiada badaniu zgodności z hipotezą prostą
najczęściej nie znamy, więc testowana hipoteza zerowa jest hipotezą złożoną, co nastręcza pewnych trudności. W poniżej opisanych testach najczęściej te parametry są estymowane z próby, z użyciem być może niestandardowych estymatorów, a statystyka testowa odpowiada badaniu zgodności z hipotezą prostą
Poniżej przedstawiamy różne testy do weryfikacji hipotezy o zgodności z rodziną rozkładów normalnych, ale wiele z prezentowanych metod może być zaadoptowanych do zagadnienia testowania zgodności z innymi rodzinami rozkładów.
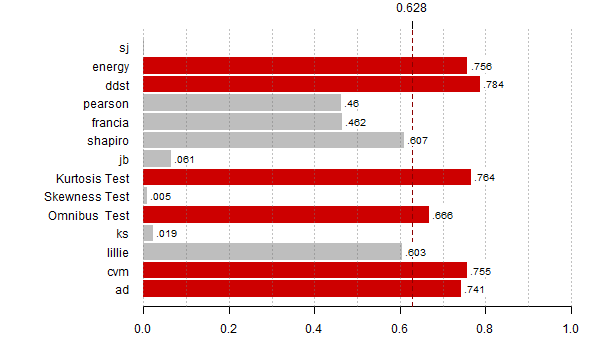
Dla większości testów przedstawiamy też przykładowe alternatywy, dla których dany test ma największą moc. Wybrane scenariusze alternatyw to jednak kropla w zbiorze możliwych odstępstw od normalności.
Naturalnym pytaniem jest ,,którego testu używać'', poniższe przykłady wykazują, że nie ma testu dobrego w każdym przypadku, ale o dwóch warto wspomnieć. Testem często stosowanym jest test Shapiro Wilka, popularny i zaimplementowany w większości pakietów statystycznych. Testem o szerokim spektrum wykrywania możliwych odstępstw jest test gładki test Neymana zaimplementowany w pakiecie R.
Testy wymienione w tym rozdziale badają zgodność z rozkładem normalnym przez ocenę odległości pomiędzy dystrybuantą empiryczną a dystrybuantą rozkładu normalnego.
Opisane w tym rozdziale testy określa się terminem ,,distribution free'', co oznacza, że rozkład statystyki testowej przy prawdziwej hipotezie zerowej nie zależy od rozkładu, z którym badana jest zgodność.
Ten test jest oparty o odległość Cramera von Misesa pomiędzy dystrybuantami empiryczną ![]() i teoretyczną
i teoretyczną ![]()
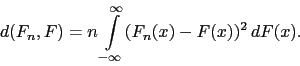 |
(1) |
Statystkę testową dla próby ![]() zbudowaną na powyższej odległości można zapisać jako
zbudowaną na powyższej odległości można zapisać jako
| (2) |
W przypadku badania zgodności z rozkładem normalnym dystrybuanta ![]() jest zastępowana przez
jest zastępowana przez
![]() dla oszacowanych parametrów średniej i wariancji. Rozkład statystyki przybliża się po uprzedniej modyfikacji [Stephens1986]
dla oszacowanych parametrów średniej i wariancji. Rozkład statystyki przybliża się po uprzedniej modyfikacji [Stephens1986]
| (3) |
Przyglądając się odległości ![]() widzimy, że ,,zauważane'' są różnice w centrum rozkładu, tam gdzie
widzimy, że ,,zauważane'' są różnice w centrum rozkładu, tam gdzie ![]() jest duża. Spodziewamy się ,,czułości'' testu dla alternatyw zniekształconych w środku rozkładu.
jest duża. Spodziewamy się ,,czułości'' testu dla alternatyw zniekształconych w środku rozkładu.
W programie R ten test jest zaimplementowany w funkcji cvm.test{nortest}.
set.seed(1313); x <- rnorm(100) library(nortest) cvm.test(x) # # Cramer-von Mises normality test # #data: x #W = 0.0607, p-value = 0.3665 # cvm.test(x)$p.value # 0.3664784
 |
![\begin{displaymath}
d(F_n, F) = n \int\limits_{-\infty}^\infty \frac{(F_n(x) - F(x))^2 }{[F(x)\; (1-F(x))]} \, dF(x).
\end{displaymath}](http://tofesi.mimuw.edu.pl/~cogito/smarterpoland/samouczki/testyNormalnosci/img20.png) |
(4) |
Statystkę testowę opartą o powyższą odległość dla próby prostej ![]() można przedstawić jako
można przedstawić jako
![\begin{displaymath}
\begin{array}{lll}
S &=& \sum_{k=1}^n \frac{2k-1}{n}\left[\l...
...1-F(x_{n+1-k})\right)\right], \\
A^2 &=& -n-S. \\
\end{array}\end{displaymath}](http://tofesi.mimuw.edu.pl/~cogito/smarterpoland/samouczki/testyNormalnosci/img21.png) |
(5) |
Podobnie jak w teście Cramera von Misesa, testując zgodność z rozkładem normalnym przyjmuje się
![]() , a rozkład statystyki testowej przybliża się po po uprzedniej korekcie [Stephens1986] (w literaturze spotyka się też inne korekty, poniżej prezentowana jest używana w programie R)
, a rozkład statystyki testowej przybliża się po po uprzedniej korekcie [Stephens1986] (w literaturze spotyka się też inne korekty, poniżej prezentowana jest używana w programie R)
| (6) |
W programie R ten test jest zaimplementowany w funkcji ad.test{nortest}.
set.seed(1313); x <- rnorm(100) library(nortest) ad.test(x) # # Anderson-Darling normality test # #data: x #A = 0.4141, p-value = 0.3301 # ad.test(x)$p.value # [1] 0.3300575
 |
Test oparty o odległość supremum pomiędzy dystrybuantami empiryczną ![]() i teoretyczną
i teoretyczną ![]()
| (7) |
Statystka testowa oparta o powyższą odległość sprowadza się do liczenia maksimum modułu różnicy dystrybuant w punktach skoku dystrybuanty empirycznej
| (8) |
Rozważa się też ważoną wersją testu Kołmogorowa Smirnowa, bardziej czułą na różnice w ogonach
Rozkład statystyki testowej można wyznaczyć w sposób dokładny (rekurencyjnie) dla prostej hipotezy zerowej, a więc dla porównania z jednym określonym rozkładem. Asymptotycznie, ta statystyka przemnożona przez ![]() ma rozkład Kołmogorowa.
Test ten pomimo łatwego opisu probabilistycznego nie jest stosowany z uwagi na moc niższą niż konkurencja.
ma rozkład Kołmogorowa.
Test ten pomimo łatwego opisu probabilistycznego nie jest stosowany z uwagi na moc niższą niż konkurencja.
W programie R ten test jest zaimplementowany w funkcji ks.test{stats}.
set.seed(1313) x <- rnorm(100) ks.test(scale(x), "pnorm") # # One-sample Kolmogorov-Smirnov test # #data: scale(x) #D = 0.0543, p-value = 0.9297 #alternative hypothesis: two-sided # ks.test(scale(x), "pnorm")$p.value # [1] 0.9297479
Ten test to modyfikacja testu Kołmogorowa-Smirnowa zaproponowana przez Huberta Lillieforsa [Lilliefors1967], pozwalająca na testowanie zgodności z całą rodziną rozkładów normalnych, bez znajomości parametrów średniej i odchylenia standardowego (test Kołmogorowa-Smirnowa pozwala na zbadanie zgodności z jednym określonym rozkładem).
Statystyka testowa w przypadku testu Lillieforsa wygląda tak samo jak w przypadku testu Kołmogorowa Smirnowa. Różnica polega na zastosowaniu innego rozkładu dla statystyki testowej (przybliżenie rozkładu dokładnego), uwzględniającego to, że hipoteza zerowa jest hipotezą złożoną.
W programie R ten test jest zaimplementowany w funkcji lillie.test{nortest} i lillieTest{fBasics}.
set.seed(1313); x <- rnorm(100) lillie.test(x)$p.value # [1] 0.6643097 lillieTest(x)@test$p.value # 0.6643097
 |
Testy oparte o dystrybuantę empiryczną można było stosować do badania zgodności z dowolnym rozkładem. Poniższe testy wykorzystują specyficzną właściwość rozkładu normalnego, tzn. zerową skośność i kurtozę równą 3 (licząc zgodnie z definicją ![]() ) lub kurtozę równą 0 (licząc zgodnie z definicją
) lub kurtozę równą 0 (licząc zgodnie z definicją ![]() ).
).
Aby łatwiej nam było opisać poniższe testy, przyjmijmy następujące oznaczenia na ![]() to k-ty centralny moment z próby, skośność i kurtozę.
to k-ty centralny moment z próby, skośność i kurtozę.
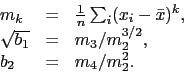 |
(9) |
Test D'Agostino (1970) za statystykę testową wykorzystuje przekształconą próbkową skośność. W celu ,,normalizacji'' rozkładu statystyki testowej stosuje się następujące przekształcenie
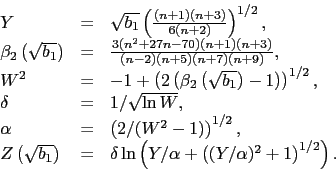 |
(10) |
Statystyką testową jest ![]() . Przy założeniu prawdziwej hipotezy zerowej ta statystyka ma asymptotyczny rozkład normalny [Agostino1970].
. Przy założeniu prawdziwej hipotezy zerowej ta statystyka ma asymptotyczny rozkład normalny [Agostino1970].
W programie R ten test jest zaimplementowany w funkcji dagoTest{fBasics}.
set.seed(1313); x <- rnorm(100) dagoTest(x)@test$p.value[2] # Skewness Test # 0.9287743
 |
Test D'Agostino za statystykę testową wykorzystuje przekształconą próbkową kurtozę.
Bazując na wynikach [Anscombe1983] w celu ,,normalizacji'' rozkładu oceny kurtozy stosuje się następujące przekształcenie
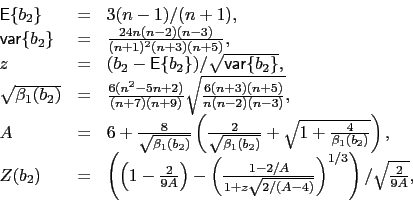 |
(11) |
gdzie
![]() ,
,
![]() to obciążenie i wariancja oceny kurtozy dla rozkładu normalnego.
to obciążenie i wariancja oceny kurtozy dla rozkładu normalnego.
Statystyką testową jest ![]() . Przy założeniu prawdziwej hipotezy zerowej ta statystyka ma asymptotyczny rozkład normalny.
. Przy założeniu prawdziwej hipotezy zerowej ta statystyka ma asymptotyczny rozkład normalny.
W programie R ten test jest zaimplementowany w funkcji dagoTest{fBasics}.
set.seed(1313); x <- rnorm(100) dagoTest(x)@test$p.value[3] #Kurtosis Test # 0.4417257
 |
Łącząc dwa powyższe testy otrzymuje się test czuły na odstępstwa od normalności zarówno w postaci niezerowej skośności jak i kurtozy istotnie różniej od 3 [Agostino1973].
Statystyką testową jest
| (12) |
Asymptotyczny rozkład tej statystyki to oczywiście rozkład ![]() .
.
W programie R ten test jest zaimplementowany w funkcji dagoTest{fBasics}.
set.seed(1313); x <- rnorm(100) dagoTest(x)@test$p.value[1] #Omnibus Test # 0.7408977
Rozszerzeniem testu D'Agostino-Pearsona na przypadek testowania zgodności z wielowymiarowym rozkładem normalnym, dla statystyki testowej opartej o kurtozę i skośność, jest test Doornika-Hansena [Doornik1994]. Jest on zaimplementowany w funkcji normality.test1{normwhn.test}, a ta implementacja pozwala też na testowanie kierunkowych alternatyw dla skośności i kurtozy, czyli że rozkład jest bardziej/mniej lewoskośny/spłaszczony niż rozkład normalny. W funkcji normality.test2{normwhn.test} zaimplementowana jest modyfikacja pozwalająca na testowanie zgodności z rozkładem normalnym przy osłabionym założeniu dotyczącym niezależności. Tzn. jest to test normalności dopuszczający słabą strukturę zależności pomiędzy obserwacjami, patrz [Velasco2004].
Więcej o teście Doornika-Hansena i innych wielowymiarowych testach normalności (np. teście Mardii, wielowymiarowym Shapiro-Francia) przeczytać można w [BiecekTrajkowski2011].
Innym testem opartym o kurtozę i skośność jest test Jarque-Bera [Jarque1987]. Statystyka testowa w przypadku tego testu ma łatwiejszą postać niż dla testu D'Agostino-Pearsona. Traci się jednak na niedokładnym oszacowaniu wartości krytycznych przy niewielkich wielkościach próby. Asymptotycznie ten test jest tak samo mocny jak test D'Agostino-Pearsona, ale na asymptotykę można liczyć jedynie w przypadku dużych prób.
Statystyka testowa ma postać
| (13) |
Asymptotyczny rozkład statystyki testowej
![]() to rozkład
to rozkład ![]() . W funkcji
. W funkcji jbTest{fBasics} zaimplementowane są też dwie inne metody liczenia p-wartości i szacowania kwantyli rozkładu statystyki JB oparte o mnożniki Lagrange, przy czym raportowane przez tę funkcję p-wartości są zaokrąglone do trzeciego miejsca po przecinku dziesiętnym. P-wartość wyznaczane przez funkcję jarqueberaTest{fBasics} nie jest zaokrąglana, jest więc podawana z większą dokładnością, ale jedynie dla przybliżenia rozkładu statystyki testowej rozkładem asymptotycznym. Zaokrąglanie p-wartości do tysięcznych uniemożliwia testowanie na poziomie istotności rzędu ![]() lub mniejszym.
lub mniejszym.
set.seed(1313); x <- rnorm(100) jbTest(x)@test$p.value # LM p-value ALM p-value Asymptotic # 0.894 0.810 0.900
Kolejne dwa testy oparte są o statystyki pozycyjne z próby. Ideę ich działania najłatwiej uchwycić przyglądając się wykresowi kwantylowemu QQ-plot.
Jednym z bardziej popularnych testów klasycznych jest test Shapiro-Wilka [Shapiro1965]. Statystyka testowa jest oparta o iloczyn skalarny unormowanych uporządkowanych statystyk porządkowych z unormowanych wartościami oczekiwanymi statystyk porządkowych. Innymi słowy
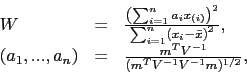 |
(14) |
gdzie
![]() to wektor wartości oczekiwanych uporządkowanych statystyk pozycyjnych w rozkładzie normalnym, a
to wektor wartości oczekiwanych uporządkowanych statystyk pozycyjnych w rozkładzie normalnym, a ![]() to macierz kowariancji tych statystyk testowych.
to macierz kowariancji tych statystyk testowych.
Wartości wektora ![]() i macierzy
i macierzy ![]() oraz rozkładu statystyki testowej pracowicie stablicowano [Sarhan1956]. W kolejnych latach proponowano różne aproksymacje tych wartości [Davis1978,Royston1982,Royston1992]. Wykorzystując tę ostatnią aproksymację wzór na statystykę testową można wyznaczyć następującym algorytmem.
oraz rozkładu statystyki testowej pracowicie stablicowano [Sarhan1956]. W kolejnych latach proponowano różne aproksymacje tych wartości [Davis1978,Royston1982,Royston1992]. Wykorzystując tę ostatnią aproksymację wzór na statystykę testową można wyznaczyć następującym algorytmem.
W pierwszym kroku wyznaczane są wartości oczekiwane statystyk porządkowych i wektor wag
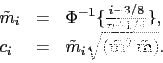 |
(15) |
W zależności od rozmiaru próby stosuje się dwa różne przybliżenia.
Dla ![]() używa się przybliżenia
używa się przybliżenia
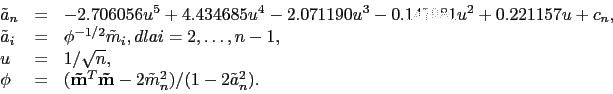 |
(16) |
Dla ![]() używa się przybliżenia
używa się przybliżenia
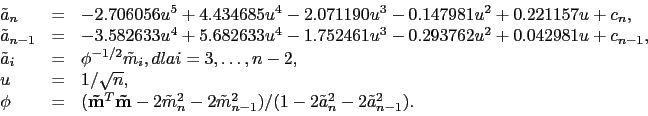 |
(17) |
Wyznaczywszy te współczynniki, statystykę testową wyznaczamy ze wzoru
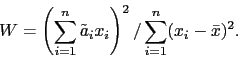 |
(18) |
Statystyka ![]() po przekształceniu przez funkcję
po przekształceniu przez funkcję ![]() ma rozkład bliski rozkładowi normalnemu o średniej
ma rozkład bliski rozkładowi normalnemu o średniej ![]() i odchyleniu standardowym
i odchyleniu standardowym ![]() [Royston1993].
[Royston1993].
Dla ![]() używa się przybliżenia
używa się przybliżenia
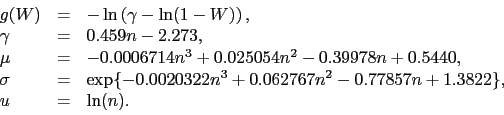 |
(19) |
Dla ![]() używa się przybliżenia
używa się przybliżenia
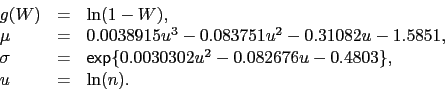 |
(20) |
Statystyka
![]() ma w przybliżeniu rozkład
ma w przybliżeniu rozkład
![]() .
.
W programie R ten test jest zaimplementowany w funkcji shapiro.test{stats}. Ta implementacja pozwala na testowanie normalności wektorów o długości od 3 do 5000 obserwacji.
set.seed(1313); x <- rnorm(100) shapiro.test(x)$p.value # [1] 0.4879372
 |
Test Shapiro-Francia jest uproszczoną wersją testu Shapiro-Wilka, w którym macierz kowariancji statystyk pozycyjnych ![]() zastąpiono przez macierz identycznościową [Shapiro1972].
Dla dużych prób ten test ma podobne zachowanie jak test Shapiro Wilka.
zastąpiono przez macierz identycznościową [Shapiro1972].
Dla dużych prób ten test ma podobne zachowanie jak test Shapiro Wilka.
Statystyką testową jest
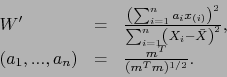 |
(21) |
Warto zauważyć, że statystyka ![]() to korelacja punktów na wykresie kwantylowym QQ-plot.
Do obliczeń wykorzystuje się wzory
to korelacja punktów na wykresie kwantylowym QQ-plot.
Do obliczeń wykorzystuje się wzory
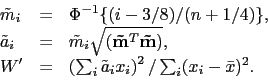 |
(22) |
Podobnie jak w teście Shapiro-Wilka statystyka
![]() jest przybliżana rozkładem normalnym o parametrach
jest przybliżana rozkładem normalnym o parametrach
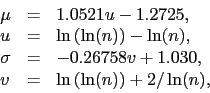 |
(23) |
Statystyka
![]() ma w przybliżeniu rozkład normalny
ma w przybliżeniu rozkład normalny
![]() .
.
W programie R ten test jest zaimplementowany w funkcji sf.test{nortest}. Ta implementacja pozwala na testowanie normalności wektorów o długości od 5 do 5000 obserwacji.
set.seed(1313); x <- rnorm(100) sf.test(x)$p.value # [1] 0.3414609
 |
Dla rozkładów o dyskretnym nośniku do badania zgodności można wykorzystać test zgodności ![]() .
W postaci ogólnej jest on zaimplementowany w programie R w funkcji
.
W postaci ogólnej jest on zaimplementowany w programie R w funkcji chisq.test(stats).
W przypadku testowania zgodności z rozkładem ciągłym, można też wykorzystać ten test, dzieląc uprzednio nośnik rozkładu na ![]() przedziałów, domyślnie w R liczbę przedziałów wyznacza się z wzoru
przedziałów, domyślnie w R liczbę przedziałów wyznacza się z wzoru ![]() . Następnie bada się zgodność z takim zdyskretyzowanym rozkładem.
. Następnie bada się zgodność z takim zdyskretyzowanym rozkładem.
Test Pearsona jest oparty o statystykę ![]()
Do przybliżenia rozkładu statystyki testowej używa się rozkładu ![]() lub
lub ![]() . W przypadku nieznanych parametrów
. W przypadku nieznanych parametrów ![]() i
i ![]() żaden z tych rozkładów nie jest dokładnym rozkładem statystyki testowej ale zaleca się wyznaczanie p-wartości z użyciem rozkładu
żaden z tych rozkładów nie jest dokładnym rozkładem statystyki testowej ale zaleca się wyznaczanie p-wartości z użyciem rozkładu ![]() .
.
W programie R ten test jest zaimplementowany w funkcji pearson.test{nortest} oraz pchiTest{fBasics}. W pierwszej z tych funkcji za wybór rozkładu asymptotycznego odpowiada opcja adjust=TRUE (![]() , domyślnie) lub
, domyślnie) lub adjust=FALSE (![]() ). W drugiej z tych funkcji liczone są dwie p-wartości, dla rozkładu
). W drugiej z tych funkcji liczone są dwie p-wartości, dla rozkładu ![]() i dla
i dla ![]() .
.
set.seed(1313); x <- rnorm(100) pearson.test(x)$p.value # [1] 0.5878833 pchiTest(x)@test$p.value # Adjusted Not adjusted # 0.5878833 0.7515082
 |
Poza wymienionymi klasycznymi testami zgodności, w literaturze znaleźć można też ,,nowoczesne'' testy w znacznym stopniu oparte na możliwościach obliczeniowych współczesnych komputerów. Poniżej przedstawiona będzie modyfikacja gładkiego testu Neymana, ciekawa metodologicznie i łatwo dostępna w programie R.
Poniższy opis statystyki testowej dotyczy badania zgodności z rodzinami rozkładów z parametrem położenia i skali, a w szczególności z rodziną rozkładów normalnych [Janic2008]. Więcej o gładkich testach znaleźć można w [Kallenberg1997].
Statystyką testową jest
| (24) |
Wybór statystyk i ich liczba wpływa na to, na jakie alternatywy ten ten będzie ,,wyczulony''. W poniżej przedstawionej implementacji, liczba ![]() jest wybierana z użyciem pewnego kryterium wyboru modelu, a
jest wybierana z użyciem pewnego kryterium wyboru modelu, a ![]() to pierwsze
to pierwsze ![]() funkcji z bazy funkcji ortonormalnych, np. bazy kosinusów lub bazy wielomianów Legendre'a. Użycie kryterium wyboru modelu do wyboru liczby
funkcji z bazy funkcji ortonormalnych, np. bazy kosinusów lub bazy wielomianów Legendre'a. Użycie kryterium wyboru modelu do wyboru liczby ![]() powoduje, że im większa próba, tym na większą liczbę alternatyw ten test będzie czuły.
powoduje, że im większa próba, tym na większą liczbę alternatyw ten test będzie czuły.
Parametry rozkładu normalnego ocenia się estymatorami
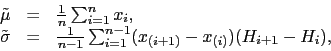 |
(25) |
gdzie ![]() to uporządkowane rosnąco statystyki porządkowe próby, a
to uporządkowane rosnąco statystyki porządkowe próby, a
![]() .
.
Statystyka testowa
![]() opisana jest szczegółowo w [Janic2008].
Wartość statystyki testowej można wyznaczyć dzięki ztablicowanym macierzom
opisana jest szczegółowo w [Janic2008].
Wartość statystyki testowej można wyznaczyć dzięki ztablicowanym macierzom
![]() . Do wyznaczania p-wartości stosuje się aproksymacje funkcji kwantylowej.
. Do wyznaczania p-wartości stosuje się aproksymacje funkcji kwantylowej.
W programie R ten test jest zaimplementowany w funkcji ddst.norm.test{ddst}.
set.seed(1313); x <- rnorm(100) ddst.norm.test(x, compute.p=TRUE) # Data Driven Smooth Test for Normality # #data: x, base: ddst.base.legendre, c: 100 #WT* = 0.0318, n. coord = 1, p-value = 0.872
 |
Do studium symulacyjnego dodano test zgodności z wielowymiarowym rozkładem normalnym (w tym przypadku jednowymiarowym), test oparty o statystykę E (patrz [Szekely2005]), czyli średnią odległość pomiędzy każdą parą obserwacji (to nie jest prawdziwa odległość w matematycznym sensie, chodzi o
![]() )
)
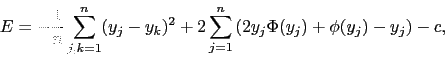
W programie R ten test jest zaimplementowany w funkcji mvnorm.etest{energy}.
set.seed(1313); x <- rnorm(100) mvnorm.etest(x, R = 999) # # Energy test of multivariate normality: estimated parameters # #data: x, sample size 100, dimension 1, replicates 999 #E-statistic = 0.4521, p-value = 0.3373
W symulacjach uwzględniono również test zgodności z rozkładem normalnym oparty o statystykę SJ (S od ,,standard deviation'' i J od ,,verage absolute deviation from the median'') [Gel2007]. Jest to test kierunkowy badający ciężko-ogonowość rozkładu, stąd też dla pewnych alternatyw moc tego testu będzie znacznie niższa niż poziom istotności.
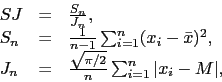 |
(26) |
W programie R ten test jest zaimplementowany w funkcji sj.test{lawstat}.
set.seed(1313); x <- rnorm(100) sj.test(x) # # Test of Normality - SJ Test # #data: x #Standardized SJ Statistic = 0.0353, ratio of S to J = 1.001, p-value = 0.4865
 |
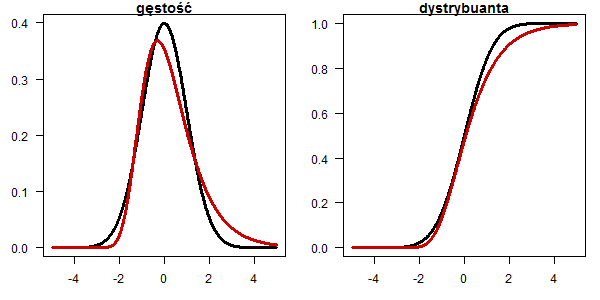
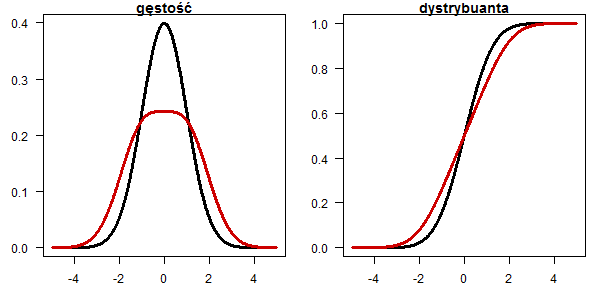
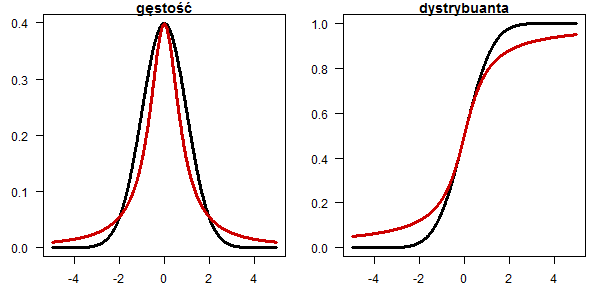
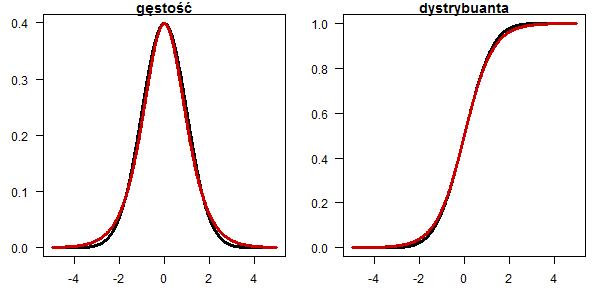
Rozkład Cauchego
x <- seq(-5,5,0.01) plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(x, dcauchy(x,0,0.8), type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, pcauchy(x,0,0.8), type="l", lwd=3, col="red3")
Rozkład Gumbela (wartości ekstremalnej)
plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(x, dgumbel(x,-0.3), type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, pgumbel(x,-0.3), type="l", lwd=3, col="red3")
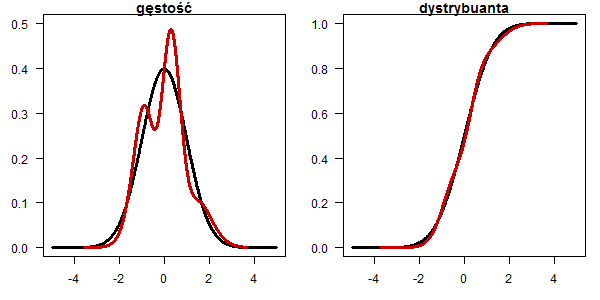
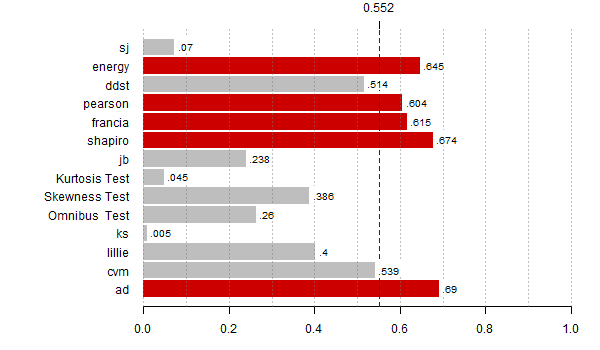
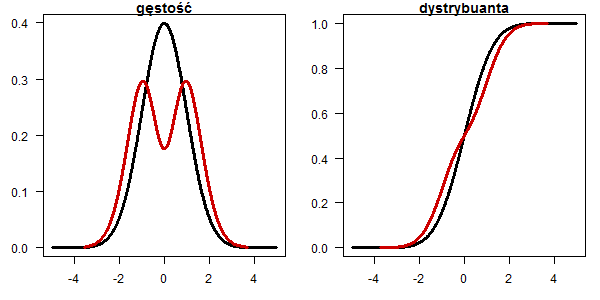
Rozkład mieszaniny dwóch rozkładów ![]() ,
, ![]()
plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(x, (dnorm(x,-1)+dnorm(x,1))/2, type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, (pnorm(x,1)+pnorm(x,-1))/2, type="l", lwd=3, col="red3")
Rozkład logistyczny
plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(x, dlogis(x,0,0.627), type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, plogis(x,0,0.627), type="l", lwd=3, col="red3")
Rozkład lognormalny
plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(x, dlnorm(x+2.2,0.83,0.5), type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, plnorm(x+2.2,0.83,0.5), type="l", lwd=3, col="red3")
Rozkład alternatywa Legendre'a rzędu 2
tx <- seq(0.0001,1-0.0001,0.0001) ty <- (ddst:::ddst.polynomial.fun[[3]](tx)+2)/2 plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(qnorm(tx)[-1], ty[-1]/diff(qnorm(tx))/10000, type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(qnorm(tx), cumsum(ty)/10000, type="l", lwd=3, col="red3")
Rozkład alternatywa Legendre'a rzędu 7
tx <- seq(0.0001,1-0.0001,0.0001) ty <- (ddst:::ddst.polynomial.fun[[7]](tx)+2)/2 plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość",ylim=c(0,0.53)) lines(qnorm(tx)[-1], ty[-1]/diff(qnorm(tx))/10000, type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(qnorm(tx), cumsum(ty)/10000, type="l", lwd=3, col="red3")
Rozkład alternatywa Legendre'a rzędu 6
tx <- seq(0.0001,1-0.0001,0.0001) ty <- (ddst:::ddst.polynomial.fun[[6]](tx)+4)/4 plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość",ylim=c(0,0.5)) lines(qnorm(tx)[-1], ty[-1]/diff(qnorm(tx))/10000, type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(qnorm(tx), cumsum(ty)/10000, type="l", lwd=3, col="red3")
Rozkład alternatywa Legendre'a rzędu 4
tx <- seq(0.0001,1-0.0001,0.0001) ty <- (ddst:::ddst.polynomial.fun[[4]](tx)+3 )/3 plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość") lines(qnorm(tx)[-1], ty[-1]/diff(qnorm(tx))/10000, type="l", lwd=3, col="red3") plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(qnorm(tx), cumsum(ty)/10000, type="l", lwd=3, col="red3")
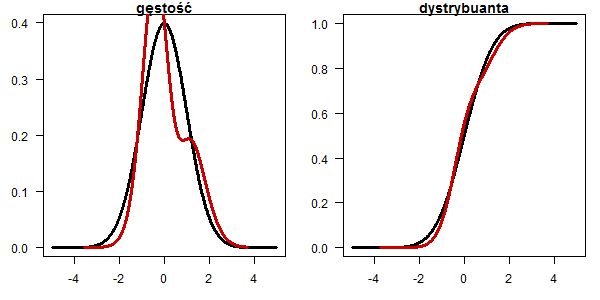
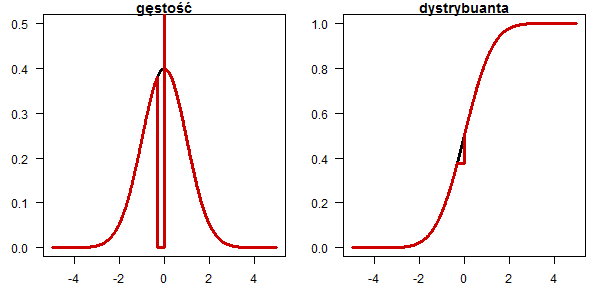
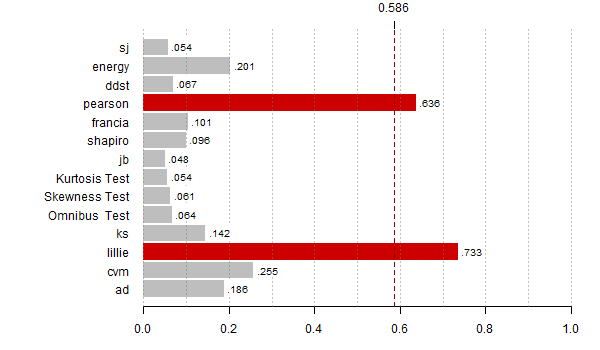
Rozkład alternatywa w której część rozkładu normalnego skupiono w punkcie
dd <- dnorm(x) dd[x < 0 & x > -0.32] = 0 dd[abs(x) < 0.001] = 100 plot(x, dnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="gęstość", ylim=c(0,0.5)) lines(x, dd, type="l", lwd=3, col="red3") pp <- pnorm(x) pp[x < 0 & x > -0.32] = pnorm(-0.32) plot(x, pnorm(x), type="l", lwd=3, las=1, ylab="",xlab="", main="dystrybuanta") lines(x, pp, type="l", lwd=3, col="red3")
library(fBasics)
library(lawstat)
library(nortest)
library(energy)
library(ddst)
#
# funkcja liczy p-wartosci dla rozważanych testów
# za wyjątkiem testu E, dla którego liczona jest wartosc statystyki testowej
zbiorTestow <- function(x) {
c(ad=ad.test(x)$p.value,
cvm = cvm.test(x)$p.value,
lillie=lillie.test(x)$p.value,
ks=ks.test(scale(x),"pnorm")$p.value,
dagoTest(x)@test$p.value,
jbTest(x)@test$p.value,
shapiro=shapiro.test(x)$p.value,
francia=sf.test(x)$p.value,
pearson=pearson.test(x)$p.value,
ddst=ddst.norm.test(x, compute.p=TRUE)$p.value,
normal.e(x),
sj.test(x)$p.value)
}
#
# scenariusze alternatyw
getData <- function(k = 1) {
switch(k,
'1'= runif(50),
'2'= rcauchy(20),
'3'= rlnorm(20),
'4'= rgumbel(60),
'5'= ifelse(runif(500)<0.5,rnorm(500),rnorm(500,2)),
'6'= ifelse(runif(300)<0.5,rnorm(300),rnorm(300,0,2)),
'7'= rnorm(25),
'8' = rchisq(45,3),
'9' = rweibull(20,0.8),
'10' = rweibull(40,1.5),
'11' = rexp(25,0.7),
'12' = ifelse(runif(1000)<0.08,rnorm(1000),rnorm(1000,0,10)),
'13' = round(rnorm(500)*5,0),
'14' = runif(500)+runif(500),
'15' = runif(1000)+runif(1000)+runif(1000),
'16' = rlogis(350),
'17' = rt(100,3),
'18' = qnorm(sample(tx,80,replace=T,prob=wx)),
'19' = qnorm(sample(tx,100,replace=T,prob=wx2)),
'20' = qnorm(sample(tx,100,replace=T,prob=wx3)),
'21' = qnorm(sample(tx,250,replace=T,prob=wx4)),
'22' = qnorm(sample(tx,1000,replace=T,prob=wx5)),
'23' = qnorm(sample(tx,100,replace=T,prob=wx6)))
}
#
# gestosci pomocnicze
tx <- seq(0.0001,1-0.0001,0.0001)
wx <- ddst:::ddst.polynomial.fun[[5]](tx)+2
wx2 <- ddst:::ddst.polynomial.fun[[3]](tx)+2
wx3 <- ddst:::ddst.polynomial.fun[[7]](tx)+2
wx4 <- ddst:::ddst.polynomial.fun[[6]](tx)+4
wx5 <- ddst:::ddst.polynomial.fun[[2]](tx)+2
wx6 <- ddst:::ddst.polynomial.fun[[4]](tx)+3
#
# poziomy istotnosci dla kolejnych testow
alfy <- c(0.05,0.01,0.01,0.05,0.05,0.05,0.01,0.01,0.01,0.05,
0.03,0.05,0.01,0.05,0.05,0.05,0.05,0.05,0.05,0.05,
0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05)
#
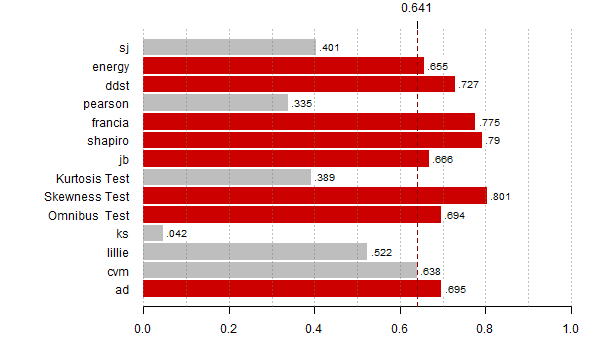
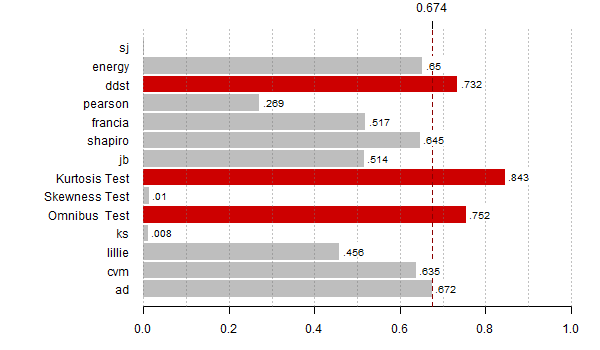
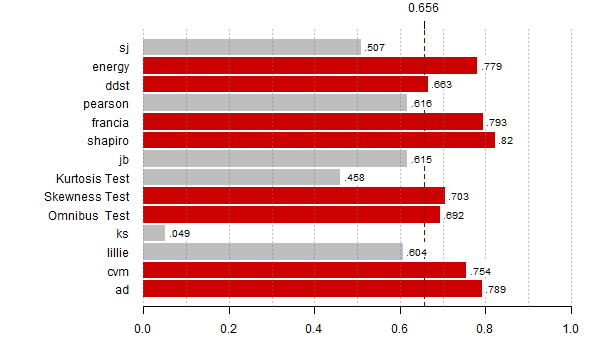
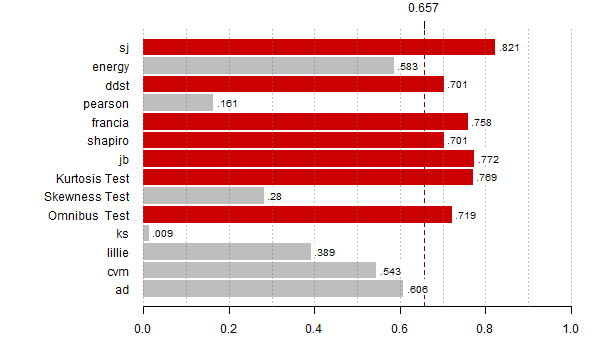
# wyznacz moce dla wszystkich alternatyw
N <- 10000
for (alte in 1:23) {
# policz p-wartosci
res <- replicate(N, zbiorTestow(getData(alte)) )
# dla testu E wyznacz empirycznie p-wartosci
n <- length(getData(alte))
res0 <- replicate(N, normal.e(rnorm(n)) )
res["energy",] <- sapply(res["energy",], function(r) (sum(r < res0) + 1)/(N+1))
# rysuj wykres do pliku pdf
pdf(paste0("moc",alte,".pdf"),9,4)
par(mar=c(3,10,2,2))
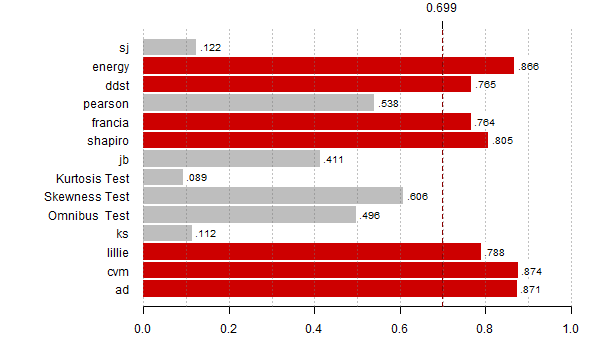
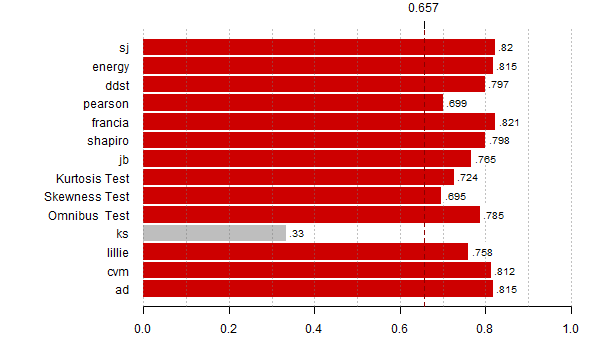
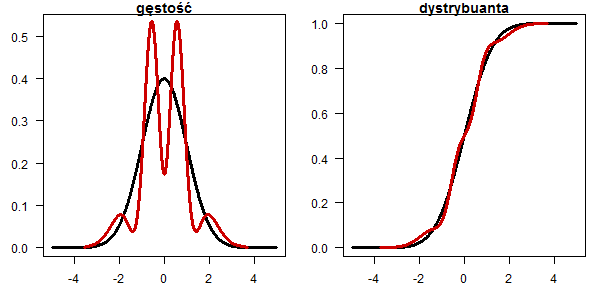
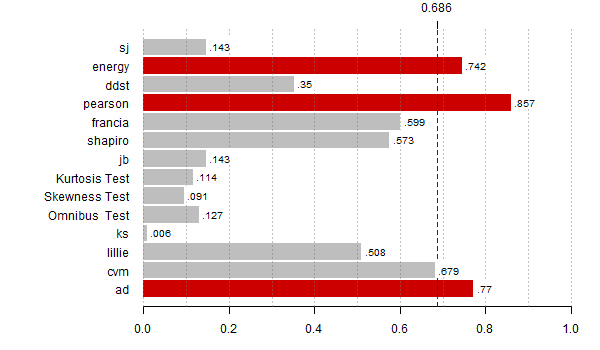
moce <- rowMeans(res < alfy[alte])
th <- max(moce,na.rm=T)*0.8
bb <- barplot(moce[-(8:9)], horiz=T,las=1, xlim=c(0,1), main="",
col=ifelse(moce[-(8:9)] > th, "red3", "grey"),
border=ifelse(moce[-(8:9)] > th, "red3", "grey"))
abline(v = seq(0,1,0.1), lty = 3, col = "#77777777")
abline(v = th, lty = 2, lwd = 1, col = "red4")
rect(moce[-(8:9)]+0.005, bb - 0.35, moce[-(8:9)]+0.08, bb + 0.4,
col="white", border="white")
text(moce[-(8:9)]+0.01, bb - 0.25, substr(as.character(round(moce[-(8:9)],3)),2,10),
adj=c(0,0), cex=0.8)
axis(3,th,round(th,3))
dev.off()
}