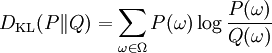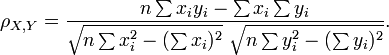Measuring distances between motifs
In MMF, the motifs comparison is realized through
comparing probability distributions. Once we describe a motif
by a proper distribution, the methods employed are:
In order to compare a pair of motifs, we need to transform their
Position Specific Score Matrices (PSSMs) into probability
distributions. MMF supports two natural ways of doing this:
-
Directly taking probabilities from motifs' Position-Specific
Probability Matrices and comparing them column-wise, referred to as
columns comparison. This is the
most natural way of comparing motifs, however it does not take into
account the information contained in the input sequences.
-
Calculating the PSSM score for each position in the input
sequences and normalizing the result into a probability
distribution, referred to as fitting on
sequences comparison. This is more computationaly
intensive, but takes into account the information contained in
the input.
Another issue that needs to be addressed is the alignment of
motifs. Since motifs can be of different length and the instances of
the same motif returned by different programs can be shifted by few
basepairs, the motifs need to be aligned before comparison. We use
ungapped alignment with the assumption that the motifs need to be
overlapping with at least one basepair.
Distributions comparison methods
Kullback-Leibler divergence (also called relative entropy or information divergence) is given by the following formula:
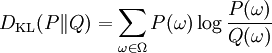
Unfortunately, this is not a true metric as it is not symmetric, nor does it fulfil the triangle inequality. That's why it is called divergence rather then metric. It is always non-negative and has no upper-bound. DKL(P||Q) returns zero if and only ifP = Q.
DPQ distance is defined as:
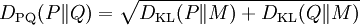 where
where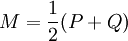
It can be interpreted as an analog of relative entropy, however it fulfills all the requirements for distance metric.
DPQ metric was introduced by Endres and Schindelin in the following paper:
DM Endres, JE Schindelin A new metric for probability distributions, Information Theory, IEEE Transactions on, Vol. 49, No. 7. (2003), pp. 1858-1860
Pearson's correlation coefficient ρX, Y between two random variablesX andY is used to measure the linear relationship between them. It is defined as a quotient of the covariance of the two variables and the product of their standard deviations:
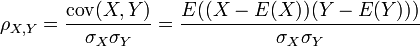 where σX2 = E(X2) − E2(X)
where σX2 = E(X2) − E2(X)
The correlation is 1 when there is a positive linear dependence and -1 in case of negative linear dependence. Zero indicates that there is absolutely no linear relationship between the variables.
In practice, correlation is measured basing on a number of samples of X and Y. If we have a series of measurements xi, yi of X andY (i = 1,2,...n), the following formula applies:
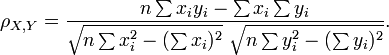
As zero is returned in case of no correlation, the coefficient is at the end converted using the following function: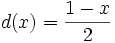 . Now 0 indicates positive linear relationship, and the range of values is [0, 1].
. Now 0 indicates positive linear relationship, and the range of values is [0, 1].
Note 1: the series of samples in MMF application are values from probability distributions (columns of PSPM or fitting on sequences values).
Note 2: the returned values significantly greater than 0.5 are very rare, as a decreasing linear relationship in comparing PSPMs' columns or positioning on input sequences would have no biological explanation.
Ways of obtaining distribution from motifs
Columns comparison is a method in which the motifs' PSPMs are compared column by column. Each pair of columns is compared using the same, previously chosen method (Kullback-Leibler divergence, DPQ distance or Pearson correlation). If one motif is longer than the other, the missing columns are filled with the background distributions. Then, the average from all columns is returned as a result.
Note: to take into account the case when motifs are shifted (e.g. ATTGCTT and TTGCTTC), the value is counted for each shift with at least one column overlapping, and the best score is chosen. Here again the missing columns are filled with background distributions.
Comparing putative occurrences in input sequences is a different approach, where the distances between motifs depend ont only on motifs' structure, but also on the input sequences. The algorithm for obtaining the distribution r(M) for motif M of width w is as following:
- Concatenate all input sequences and their complementary sequences into one, long sequence S of length s
- For each position j in the sequence S, where j=1,2,..,s-w+1, count the score of occurrence of motif M on this position (calculated as the probability of generating the word S[j..j+w-1] from the PSPM associated with motif M)
- Such an obtained sequence of values is normalized so that the sum equals one. It is possible if at least one score was non-zero, but applying the pseudocounts to the distributions beforehand ensures that all values are positive (however, many will be very close to zero)
In order to compare two motifs, M1,M2, we apply a previously chosen method for comparing probability distributions (e.g. Pearson correlation) to r(M1), r(M2).
Note: as previously, we need to take into account shifted motifs. To this end, we compare shifted distributions with appropriately trimmed ends.
Example: suppose we have an input of total 1000 bp, and two motifs: 5 and 8 bp long. There are 12 possible shifts of one motif against the other, hence there will be 12 comparisons of distributions of lengths from 993 to 996
back